队列与循环队列

Breeze Shane大约 7 分钟DataStructuresAndAlgorithmsData Structures and Algorithms

队列简称队，也是一种操作受限的线性表，只允许在表的一端进行插入，而在另一端进行删除。我们称向队列中插入元素为入队，从队列中删除元素为出队或离队。

对于队列有以下三个概念：

  1. 队首：允许删除的一端，又称队头。
  2. 队尾：允许插入的一端。
  3. 空队列：不含任何元素的空表。

考研中可直接使用的栈的基本操作

  1. InitQueue(&Q): 初始化队列
  2. QueueEmpty(Q): 判队列空
  3. EnQueue(&Q, x): 入队
  4. DeQueue(&Q, &x): 出队
  5. GetHead(Q, &x): 读队首元素

队列的操作特性是先进先出。

队列的顺序存储

如图所示：

结构定义代码如下：

typedef int ElemType;
enum { MAX_SIZE = 50 };
typedef struct {
	ElemType data[MAX_SIZE];
	int head, tail;
    // int tag; // 视情况使用
    // int size; // 视情况使用
} SqQueue, *PSqQueue;

初始时，Q.head == Q.tail == 0。 入队：队不满时，先在队尾插入元素，后将队尾指针后移一个单位。 出队：队不空时，先取队首元素，再将队首指针后移一个单位。

存在的问题

如果我们就使用上面的队列进行一系列操作后，tail指针指向了表的最后一个元素。这时即使队列未满，我们仍可发现我们无法按照上面的思路继续进行插入（发生了“上溢出”，而这个情况的溢出不是真正的溢出，故而是一种“假溢出”）。因此为了解决这个问题，循环队列应运而生。

队列的顺序存储变种——循环队列

把存储队列元素的表从逻辑上视为一个环，将顺序队列臆造为一个环状的空间，我们称之为循环队列。当队首指针Q.head == MAX_SIZE-1时，再前进一个位置就自动归0，而要实现这个效果，我们可以利用求余运算来实现。

如图所示：

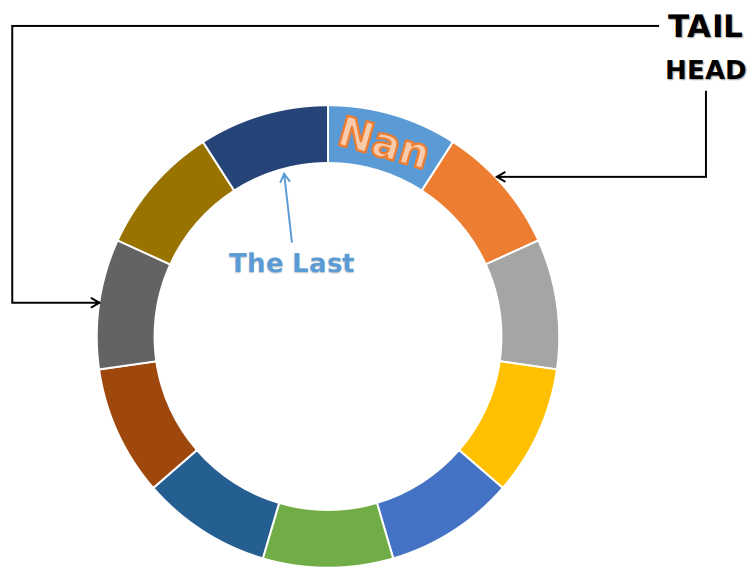
初始时：Q.head == Q.tail == 0。 队首指针后移一个位置：Q.head = (Q.head + 1) % MAX_SIZE。 队尾指针后移一个位置：Q.tail = (Q.tail + 1) % MAX_SIZE。 队列长度：(Q.tail - Q.head + MAX_SIZE) % MAX_SIZE。

队列判空

如果我们使用Q.head == Q.tail作为队列判空条件的话，当入队速度快过出队速度的时候，队尾指针会很快赶上队首指针，这时候会发现队满的情况也是满足Q.head == Q.tail条件的，因此为了区分队空还是队满，我们通常有三种处理方式：

  1. 牺牲一个单元来区分队空与队满：这是一种较为普遍的做法：入队时少用一个队列单元，约定以“队首指针在队尾指针的下一位置”作为队满的标志。 队满条件：(Q.tail + 1) % MAX_SIZE == Q.head。 队空条件：Q.head == Q.tail。
  2. 类型中增设表示元素个数的数据成员： 队满条件：Q.size == MAX_SIZE。 队空条件：Q.size == 0。
  3. 类型中增设tag数据成员：若因出队导致Q.head == Q.tail，则为队空，tag赋值为0；若因入队导致Q.head == Q.tail，则为队满，tag赋值为1。 队满条件：Q.tag == 1。 队空条件：Q.tag == 0。

结构定义

typedef int ElemType;
enum { MAX_SIZE = 50 };
typedef struct {
    ElemType data[MAX_SIZE];
    int head, tail;
} SqQueue, *PSqQueue;

初始化

void InitQueue(PSqQueue Q){
    Q->tail = Q->head = 0;
}

队列判空

int IsEmptyQueue(PSqQueue Q){
    return Q->tail == Q->head;
}

队列判满

int IsFullQueue(PSqQueue Q){
    return (Q->tail + 1) % MAX_SIZE == Q->head;
}

入队

int EnSqQueue(PSqQueue Q ,ElemType x){
    if ( IsFullQueue(Q) ) return -1;
    Q->data[Q->tail] = x;
    Q->tail = (Q->tail + 1) % MAX_SIZE;
    return 1;
}

出队

ElemType DeSqQueue(PSqQueue Q){
    if ( IsEmptyQueue(Q) ) return -1;
    ElemType tmp = Q->data[Q->head];
    Q->head = (Q->head + 1) % MAX_SIZE;
    return tmp;
}

读取

ElemType GetHead(PseqQueue Q){
    if ( IsEmptyQueue(Q) ) return -1;
    return Q->data[Q->head];
}

获取队列长度

ElemType GetLength(PSqQueue Q){
    return (Q->tail - Q->head + MAX_SIZE) % MAX_SIZE;
}

队列的链式存储

队列的链式表示称为链队列。它实际上是一个同时带有队首指针和队尾指针的单链表，其中头指针指向队首结点，为指针指向队尾结点。

结构定义为：

typedef int ElemType;
typedef struct LinkNode{
    ElemType data;
    struct LinkNode* next;
} LinkNode;

typedef struct {
    LinkNode *head, *tail;
}* LinkQueue;

当Q.head == NULL且Q.tail == NULL时，链队列为空。出队时，首先判断队列是否为空，若不空则取出队首元素并将其从链表中删除，并让Q.head指向下一个结点（若出队时的结点为链表中最后一个结点，则需要让Q.head和Q.tail都置为NULL）；入队时，建立一个新结点并初始化，然后将其插入到链表的尾部，并让Q.tail指向这个结点（若入队时的结点为链表中的第一个结点，则需要让Q.head和Q.tail都指向这个结点）。

如果按照这个方式来写的话插入和删除都需要单独考虑队列为空的情况，操作上有所不同，因此一般将链式队列设计成带有头结点的单链表，从而达成统一删除和插入操作的目的。

初始化

void InitLQueue(LinkQueue Q){
    Q->head = Q->tail = (LinkNode*) malloc(sizeof (LinkNode));
    Q->head->next = NULL;
}

队列判空

int IsEmptyLQueue(LinkQueue Q){
    return Q->head == Q->tail;
}

入队

void EnLQueue(LinkQueue Q, ElemType x){
    LinkNode* s = (LinkNode*) malloc(sizeof (LinkNode));
    s->data = x, s->next = NULL;
    Q->tail->next = s;
    Q->tail = s;
}

出队

int DeLQueue(LinkQueue Q, ElemType* x){
    if ( IsEmptyLQueue(Q) ) return -1;
    LinkNode* p = Q->head->next;
    *x = p->data;
    Q->head->next = p->next;
    if (Q->tail == p) Q->tail = Q->head;
    free(p);
    return 1;
}

队列的拓展——双端队列

双端队列是指允许两端都可以进行入队和出队操作的队列，其元素的逻辑结构仍然是线性结构。我们将队列的两端分别称为前端和后端。

在双端队列入队时前端进的元素排列在队列中后端进的元素前面，后端进的元素排列在队列中前端进的元素后面；在上端队列出队时无论前端还是后端出队，先出的元素排列在后出的元素前面。

若给双端队列加以限制，我们又可以得到两种双端队列：

  1. 输出受限的双端队列：允许在一端进行插入和删除，但在另一端只允许插入的双端队列称为输出受限的双端队列。
  2. 输入受限的双端队列：允许在一端进行插入和删除，但在另一端只允许删除的双端队列称为输入受限的双端队列。若限定双端队列从某个端点插入的元素只能从该端点删除，则该双端队列就蜕变为两个栈底相邻接的栈。
𝕭𝖗𝖊𝖊𝖟𝖊 𝕾𝖍𝖆𝖓𝖊 𝕭𝖑𝖔𝖌
Copyright © 2024 Breeze Shane