利普希茨连续——Lipschitz Continuity

参考资料：利普希茨连续 - 维基百科

定义

对于在实数集的子集的函数$f\colon D\subseteq \mathbb {R} \to \mathbb {R}$，若存在常数$K$，使得$|f(a)-f(b)|\leq K|a-b|\quad \forall a,b\in D$，则称$f$符合利普希茨条件，对于$f$最小的常数$K$称为 $f$的利普希茨常数。可以近似将优化复杂函数的问题，转化为二次规划问题。

若$K<1$，$f$称为收缩映射。

利普希茨条件也可对任意度量空间的函数定义：

给定两个度量空间$(M,d_{M}),(N,d_{N}),U\subseteq M$。若对于函数$f:U\to N$，存在常数$K$使得$d_{N}(f(a),f(b))\leq Kd_{M}(a,b)\quad \forall a,b\in U$ 则说它符合利普希茨条件。

若存在$K\geq 1$使得${\frac{1}{K}}d_{M}(a,b)\leq d_{N}(f(a),f(b))\leq Kd_{M}(a,b)\quad \forall a,b\in U$ 则称$f$为双李普希茨(bi-Lipschitz)。

用处

可以近似将优化复杂函数的问题，转化为二次规划问题。

如果有$\nabla f$是Lipschitz连续的，则$\forall x,y,\quad f(y)\leq f(x)+\nabla f(x)^T(y-x)+{L\over2}||y-x||_2^2$，其中$L$为Lipschitz常数。即可以将优化复杂的函数$f(y)$等价地优化它的上界。

皮卡-林德洛夫定理

若已知$y(t)$有界，$f$符合利普希茨条件，则微分方程初值问题$y'(t)=f(t,y(t)),y(t_{0})=y_{0}$刚好有一个解。

在应用上，$t$通常属于一有界闭区间（ 如 $[0,2 \pi ]$ ）。于是$y(t)$必有界，故$y$有唯一解。

性质

1. 符合利普希茨条件的函数连续，实际上一致连续。
2. 双李普希茨(bi-Lipschitz)函数是单射。
3. Rademacher定理：若$A\subseteq {\mathbb {R}}^{n}$且$A$为开集，$f:A''\to {\mathbb {R}}^{n}$符利普希茨条件，则$f$几乎处处可微。
4. Kirszbraun定理：给定两个希尔伯特空间$H_{1},H_{2}$，$U\in H_{1}$，$f:U\to H_{1}$符合利普希茨条件，则存在符合利普希茨条件的$F:H_{1}\to H_{2}$，使得$F$的利普希茨常数和$f$的相同，且$F(x)=f(x)\quad \forall x\in U$。

几何意义

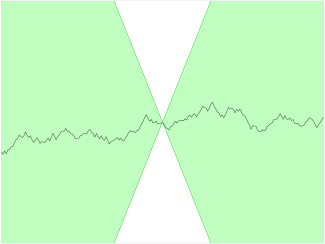
对于利普希茨连续函数，存在一个双圆锥(白色)其顶点可以沿着曲线平移，使得曲线总是完全在这两个圆锥外。

用公式的描述

$$||\nabla f(x)-\nabla f(y)|| \leq L||x-y||,\quad x,y\in R^n$$

可以描述为函数$f(x)$二次可微，且Hessian矩阵在$R^n$上有界。