Generative Adversarial Networks

Breeze Shane大约 14 分钟

经过接受GAN的洗礼，我感觉我整个人都变得“睿智”了。。。

一、什么是GAN？

GAN，Generative Adversarial Networks的简称，译名为生成对抗网络。顾名思义，该模型主要聚焦数据生成的相关问题，最早的相关资料出现在2014年的一篇论文中，相对算是较新的一种机器学习方向，近期依旧热门。而这一切正是因为GAN在一些领域上表现效果惊人而备受关注。从学习方式分类上去看，普遍认为GAN属于无监督学习（少部分人认为属于弱监督学习，另外也有些情况是有监督学习，这个仁者见仁智者见智的事不必追究）。

在今天这个DL火热的时期，数据集匮乏的问题日益凸显，越来越多的数据难于收集、筛选，这也会凸显监督学习的局限性，因为缺乏数据集意味着无法进行学习。生成对抗网络的诞生，为减缓数据资源匮乏、质量低下的问题提供了一种思路、一种解决方案。因此有人据此认为GAN大有前景。

二、GAN能做什么？效果如何？

当下的GAN已经可以做许多事，生成图像、提高图像清晰度、生成动画、生成视频、生成音乐、风格迁移、图像融合、图像修复等等，并且表现十分出色。

学习过程中的第一个GAN是2014年提出的最原始的GAN，其运行效果如下图：

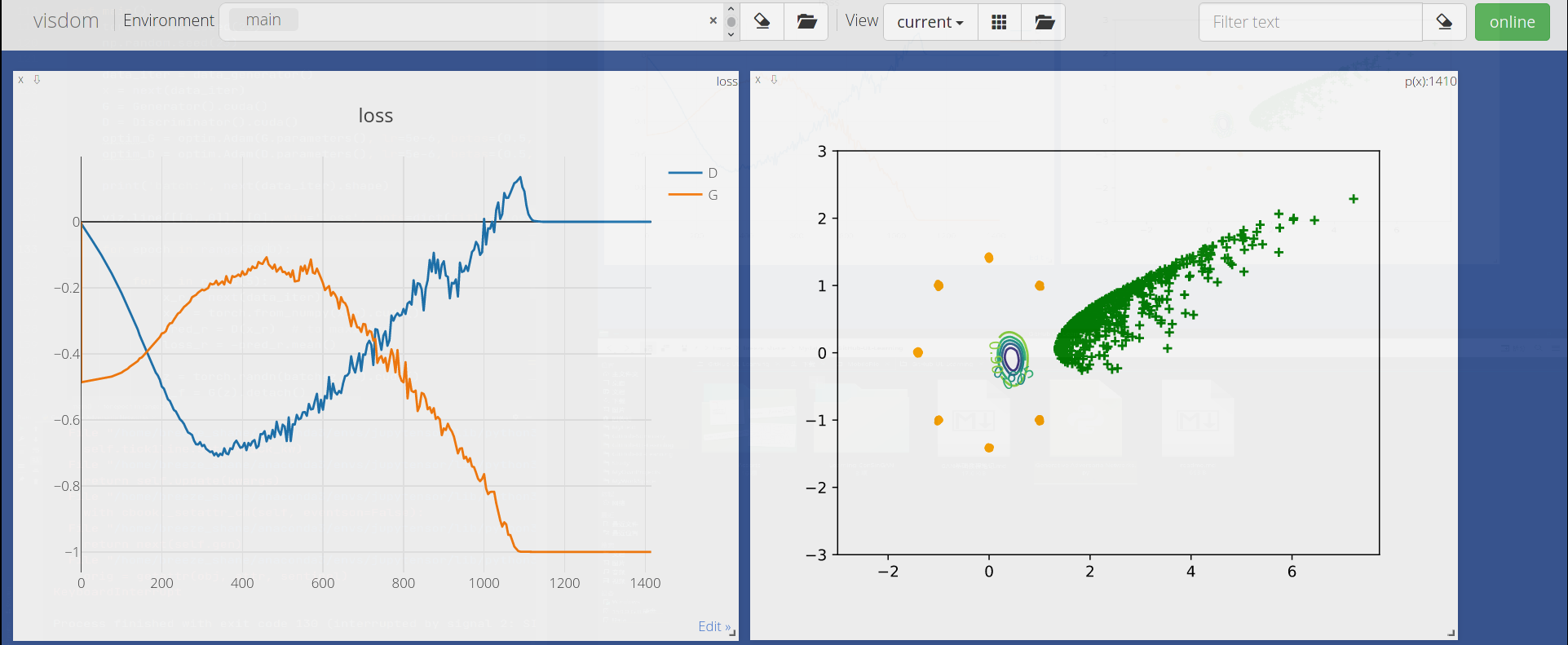
不难发现它表（GAN）现（de）糟（piào）糕（liàng），出现了严重的欠拟合和过拟合，实在让人大跌眼镜。

虽然只是个简单的GAN网络模型，但局限性非常多，原始GAN最大的缺点是训练不稳定，很可能上次运行效果颇佳，下次就令人大失所望，何况这种问题并不是设置种子、调整参数就可以改善的。因此此后将进一步学习WGAN来解决这一问题。

经过重复实验几次，均发现该网络可以良好地收敛，不会因随机性问题导致前者不稳定问题。

三、GAN的组成是什么？

GAN主要由两部分组成，一是生成器，二是判别器。但GAN并不仅局限于此，可以另外有其他部分，我有在考虑引入预训练的模型和深度网络模型从而完成相应的更复杂的问题。不论如何，GAN网络都会有这两部分，两者不可或缺。

四、GAN的原理是什么？

GAN的基本思路和形式是生成器和判别器之间的博弈。为了能生成良好的数据，具有判别能力的判别器成了一种必须。因此训练顺序已经很明显了，应该优先训练判别器，而后再训练生成器「但现在来看，其实有一同训练的」。GAN的两部分被设计成天然敌对的状态，生成器要欺瞒判别器，而判别器要识破生成器，两者因这一关系的存在而水平不断提高（这和生物学上的共同进化有异曲同工之妙），最终生成器可以达到以假乱真的程度。而判别器仅仅是附属陪同训练的网络，并不是人们真正需要的。

根据2014年最初的GAN论文，目标函数的定义如下：

\begin{aligned} \underset{G}{\min} \underset{D}{\max}L(G,D)&=E_{x\sim P_r(x)}[\log D(x)]+E_{z\sim P_z(z)}[\log (1-D(G(z)))]\\ &=E_{x\sim P_r(x)}[\log D(x)]+E_{x\sim P_g(x)}[\log (1-D(x))] \end{aligned}

注意：图中的 $E_{x \sim {P}_{r}(x)}$ 是指识别真实图像符合标准的期望，而 $E_{x\sim P_{g}(x)}$ 是指生成图像符合标准的期望

为什么要这样设计目标函数？

这里我们就要再重新审视一下GAN，它的本质究竟是什么？

鉴别器和生成器的根本任务分别是：使用鉴别器来学习训练数据集所服从的高维概率分布，并能够给出任意一个样本服从该分布的概率值；使用生成器生成随机样本，将其输入到鉴别器内来计算概率。如果得到的概率越大，说明该样本来自该分布的可能性越高，这意味着生成的数据也越接近逼真。

那么鉴别器要如何确定训练数据集所服从的高维概率分布呢？

概率论上有这样的一种方法，给定 $n$ 个采样和它所对应的某种观测下的结果，我们可以为它们附加一个参数 $\theta$ ，通过联立这些方程组，我们可以确定 $\theta$ 的可能值所组成的集合，并从中选取可能性最大的参数值来确定似然函数的形式，这种方法就称作最大似然估计方法。

若随机变量 $X$ 服从某种分布，则对应的概率分布的形式可以隐式确定，我们可以使用一个参数来隐式表示。这样我们就可以得到 $P(X;\theta)$ ，通过计算采样和其对应的结果可以确定参数的最大可能值。

回到GAN这里，我们已经设定生成器和鉴别器的对抗性关系，因此我们可以这样设计目标函数：

对于任意一个样本 $x$ ，其对应的似然函数为：

f_d(x)=[D_w(x)]^y[1-D_w(x)]^{1-y}

取所有样本可以得到总似然函数为：

f_D^*(x)=\prod^{n_1}_{i=1}[D_w(x_{data})^i]\prod^{n_2}_{j=1}[1-D_w(x_g)]^j

其中 $n_1$ 表示训练数据集的样本容量， $n_2$ 表示生成数据集的样本容量。

为了便于进行线性运算我们需要做相应的处理，首先取对数，将乘法运算更换为加法运算，得到：

\begin{aligned} f_D^{**}(x)&=\log\big\{\prod^{n_1}_{i=1}[D_w(x_{data})^i]\prod^{n_2}_{j=1}[1-D_w(x_g)]^j\big\} \\ &=\sum^{n_1}_{i=1}\log[D_w(x_{data})^i]+\sum^{n_2}_{j=1}\log[1-D_w(x_g)]^j \end{aligned}

接着我们将总似然函数最大化得到：

f_D^{***}(x)=\max_w\big\{ \sum^{n_1}_{i=1}\log[D_w(x_{data})^i]+\sum^{n_2}_{j=1}\log[1-D_w(x_g)]^j \big\}

最后我们选取其等价形式，就可以得到最终的目标函数：

f_D(x)=\max_w \big\{\mathbb{E}_{x\sim P_{data}(x)}\log[D_w(x_{data})^i]+\mathbb{E}_{x\sim P_{g}(x)}\log[1-D_w(x_g)]^j \big\}

并且针对期望的求法有这个公式（后面推导要用到）：

E[f(x)]=\int p(x)f(x)dx

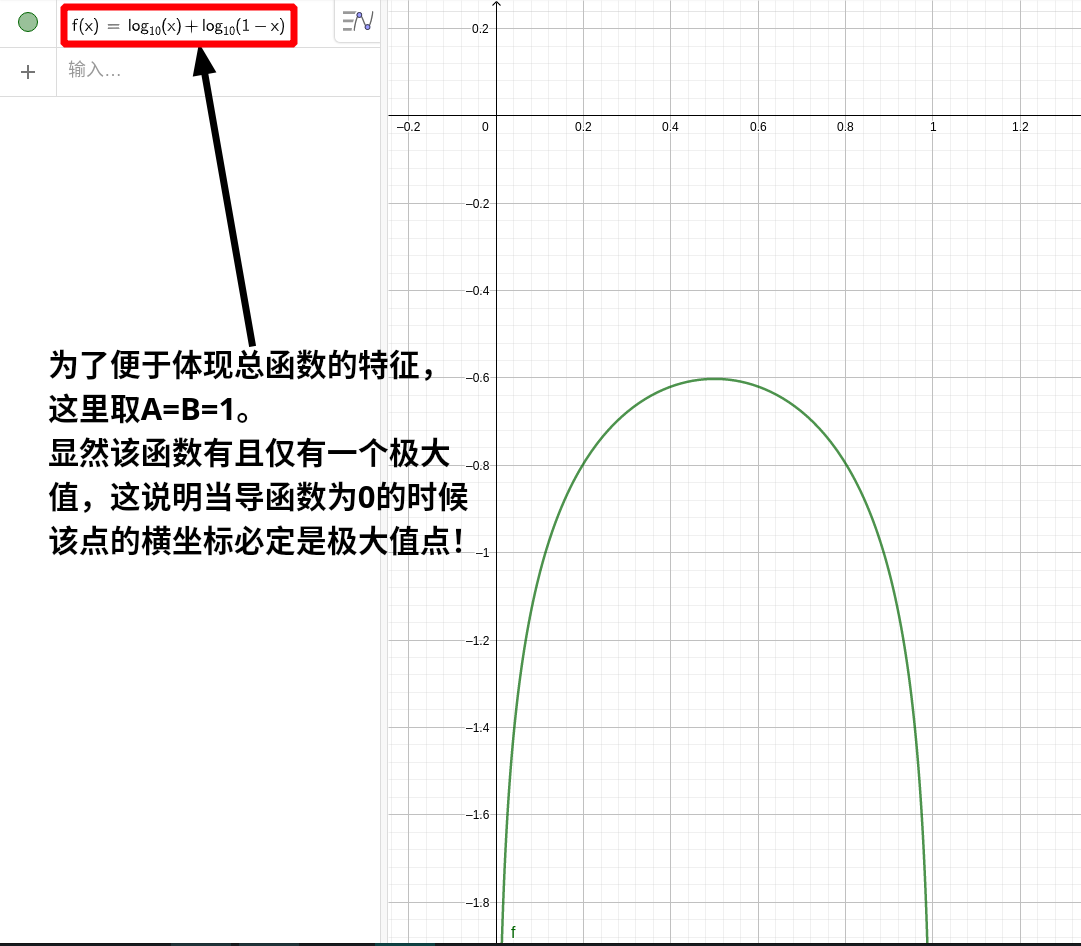
从这个总公式可以看出，min和max的相互矛盾已经天然地设计了敌对关系——D增大意味着判别能力增强，从而在识别真实图像符合标准的期望增大的同时导致生成图像符合标准的期望减损，这与最终需求是相矛盾的，而G减小会导致生成图像符合标准的期望又回升，因此最终可以确定这是一种损失函数。

确定判别器的数学表达式现在成了必须：

要注意，这里是针对max而求，G暂且还是固定的常量，因此问题被转换成了求最大值的问题：

\begin{align*} V(G,D)&=\int_xp_r(x)\log(D(x))dx+\int_zp_z(z)\log(1-D(G(z)))dz\\ &=\int_xp_r(x)\log(D(x))dx+p_g(x)\log(1-D(x)) dx\\ &\text{设}f(\lambda)=\varphi\log\lambda+\psi\log(1-\lambda)\text{,其中}\lambda=D(x),\varphi=p_r(x),\psi=p_g(x)\\ \text{则}f^\prime(\lambda)=&\frac{\varphi}{\lambda\ln10}-\frac{\psi}{(1-\lambda)\ln10}=\frac{1}{\ln10}\big({\varphi\over\lambda}-{\psi\over1-\lambda}\big)={1\over\ln10}\cdot\frac{\varphi-(\varphi+\psi)\lambda}{(1-\lambda)\ln10}\\ &\qquad\,\,\, \text{令}f^\prime(\lambda)=0\text{,则}\varphi-(\varphi+\psi)\lambda=0\\ &\therefore\lambda=\frac{\varphi}{\varphi+\psi}\text{即}D(x)=\frac{p_r(x)}{p_r(x)+p_g(x)} \end{align*}

「注」： $P_r(x)$ 和 $P_g(x)$ 在每一个确定的 $x$ 中都有确定的常数，因此求导时被看作常量。

判别器的推导完成，需要做的是后续的损失函数的推导，用到了JS散度和KL散度的问题，这里给出相应定义：

D_{KL}(p||q)=\int_x p(x)log\frac{p(x)}{q(x)}dx

D_{JS}= \frac{1}{2}D_{KL}(p||\frac{p+q}{2})+\frac{1}{2}D_{KL}(q||\frac{p+q}{2})

这两者的图像如下：

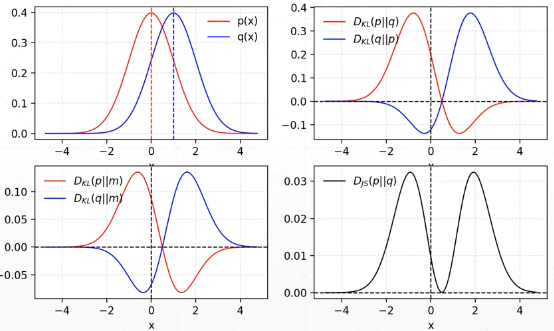
需要的损失函数是关于JS散度的，确定这一表达式，损失函数才能真正落实使用。

\begin{align*} D_{JS}&= {1\over2}D_{KL}(p||\frac{p+q}{2})+{1\over2}D_{KL}(p||\frac{p+q}{2})\\ &={1\over2}\int p_r(x)\log{2p_r\over p_r+p_g}dx+{1\over2}\int p_g(x)\log{2p_g\over p_r+p_g}dx\\ &={1\over2}\big(\log2\int p_r(x)+\int p_r(x)\log{p_r\over p_r+p_g}dx \big)+{1\over2}\big(\log2\int p_g(x)+\int p_g(x)\log{p_g\over p_r+p_g}dx\big)\\ &={1\over2}(2\log2+\int p_r(x)\log\frac{p_r}{p_r+p_g}+p_g(x)\log\frac{p_g}{p_r+p_g}dx) \\ &={1\over2}(2\log2+L(G,D)) \end{align*}

因此得知损失函数和JS散度存在如下关系：

L(G,D)=2D_{JS}(P_r||P_g)-2log2

理论指导实践。严格论证才能真正保证模型的严谨性，具有准确性、可信度与说服力。

五、GAN如何实现？

此部分共享了相关代码，主要用于构建原始GAN网络。参考资料open in new window

import torch
from torch import nn, optim, autograd
import numpy as np
import visdom
import random
from torch.nn import functional as F
from matplotlib import pyplot as plt

这里交代了所有需要的支持运行库，其中visdom是torch的基于Web平台开发的一种可视化图形绘制工具，支持实时动态更新绘制。

另外，from torch.nn import functional as F这里其实是用不上的，原作者写上这个可能是出于其他考虑，至少在纯粹的GAN这里是用不了的，介意者可删除。

h_dim = 400
batchsz = 512
viz = visdom.Visdom()


class Generator(nn.Module):
    def __init__(self, hide_layer=2):
        super(Generator, self).__init__()

        self.net = nn.Sequential(
            nn.Linear(hide_layer, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, 2),
        )

    def forward(self, z):
        output = self.net(z)
        return output


class Discriminator(nn.Module):

    def __init__(self, hide_layer=2):
        super(Discriminator, self).__init__()

        self.net = nn.Sequential(
            nn.Linear(hide_layer, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, 1),
            nn.Sigmoid(),
        )

    def forward(self, x):
        output = self.net(x)
        return output.view(-1)

这里开始设定判别器和生成器的规范类，原作者在设计网络结构的时候在第一层输入层是直接设定为（2, h_dim）矩阵，然而原作者提及这里的2可以改成其他数据，这只是设定了隐藏层层数（原作者的说法如此，这种说法依然尚存疑点。）

阿航和小蔡建议这里直接设置参数。这一建议获得采纳的原因在于它可以增强GAN的通用性，可以在一些特定场景下自由设置相应参数。参考ConSinGAN的实例可以知道，设置默认参数值的方式非常常见。

另外生成器的规范类定义中针对net的定义，最后一层的输出是一个(h_dim, 2)矩阵，这里的2则和前面的含义不同，它是指输出数据的维度（原作者的解释是这样）。判别器中的最后一层同理。

def data_generator():
    scale = 2.
    centers = [
        (1, 0),
        (-1, 0),
        (0, 1),
        (0, -1),
        (1. / np.sqrt(2), 1. / np.sqrt(2)),
        (1. / np.sqrt(2), -1. / np.sqrt(2)),
        (-1. / np.sqrt(2), 1. / np.sqrt(2)),
        (-1. / np.sqrt(2), -1. / np.sqrt(2)),
    ]
    centers = [(scale * x, scale * y) for x, y in centers]

    while True:
        dataset = []

        for i in range(batchsz):
            point = np.random.randn(2) * 0.02
            center = random.choice(centers)
            point[0] += center[0]
            point[1] += center[1]
            dataset.append(point)

        dataset = np.array(dataset).astype(np.float32)
        dataset /= 1.414
        yield dataset

这里设定了生成数据的方法，原作者避开广泛使用的MNIST数据集，而采用了高斯模型数据集。

这段代码有一个地方挺有趣：centers = [(scale * x, scale * y) for x, y in centers]

这种写法被一些人戏称为Python倒装句写法（尚未查证是否被广泛接受）。这行代码与下面的代码等效：

centers = []
for x, y in centers:
    _ = (scale * x, scale * y)
    centers.append(_)

不过显然前者的写法要简洁得多了。

值得注意的是最后一行的yield，其作用是保存循环的状态，会保存上一次的运行状况，下一次开始循环的时候会从上一次停止的地方继续，而不是重新开始，因此原作者写死循环依然可以正常运行。

def generate_image(D, G, x_r, epoch):
    N_POINTS = 128
    RANGE = 3
    plt.clf()
    x_r = x_r.cpu()


    points = np.zeros((N_POINTS, N_POINTS, 2), dtype='float32')
    points[:, :, 0] = np.linspace(-RANGE, RANGE, N_POINTS)[:, None]
    points[:, :, 1] = np.linspace(-RANGE, RANGE, N_POINTS)[None, :]
    points = points.reshape((-1, 2))
    # (16384, 2)
    # print('p:', points.shape)

    # draw contour
    with torch.no_grad():
        points = torch.Tensor(points).cuda() # [16384, 2]
        disc_map = D(points).cpu().numpy() # [16384]
    x = y = np.linspace(-RANGE, RANGE, N_POINTS)
    cs = plt.contour(x, y, disc_map.reshape((len(x), len(y))).transpose())
    plt.clabel(cs, inline=1, fontsize=10)
    # plt.colorbar()


    # draw samples
    with torch.no_grad():
        z = torch.randn(batchsz, 2).cuda() # [b, 2]
        samples = G(z).cpu().numpy() # [b, 2]
    plt.scatter(x_r[:, 0], x_r[:, 1], c='orange', marker='.')
    plt.scatter(samples[:, 0], samples[:, 1], c='green', marker='+')

    viz.matplot(plt, win='contour', opts=dict(title='p(x):%d' % epoch))

这部分是图形化处理的部分，由于学习GAN为主要目的，更好的做法是先暂时不要理会这里的问题，将更多的问题聚焦GAN上面，而不是要在里浪费更多的精力。时间充裕的情况下再学习也不迟。

虽然学会可视化处理是一种硬性要求，迟早要学，至少现在它还不是重点。

事实上如果想学习可视化处理，在这里学习并不是什么明智的做法。

def main():
    torch.manual_seed(23)
    np.random.seed(23)

    data_iter = data_generator()
    x = next(data_iter)
    G = Generator().cuda()
    D = Discriminator().cuda()
    G.apply(weights_init)
    D.apply(weights_init)
    optim_G = optim.Adam(G.parameters(), lr=5e-6, betas=(0.5, 0.9))
    optim_D = optim.Adam(D.parameters(), lr=5e-6, betas=(0.5, 0.9))

    print('batch:', next(data_iter).shape)

    viz.line([[0, 0]], [0], win='loss', opts=dict(title='loss', legend=['D', 'G'])) # 可视化处理，可忽略。

    for epoch in range(1500):

        for _ in range(5):
            x_r = next(data_iter)
            x_r = torch.from_numpy(x_r).cuda()
            pred_r = D(x_r)  # to maximize
            loss_r = -pred_r.mean()

            z = torch.randn(batchsz, 2).cuda()
            x_f = G(z).detach()
            pred_f = D(x_f)
            loss_f = pred_f.mean()

            loss_D = loss_r + loss_f

            optim_D.zero_grad()  # clear to zero
            loss_D.backward()
            optim_D.step()

        z = torch.randn(batchsz, 2).cuda()
        x_fake = G(z)
        pred_fake = D(x_fake)
        loss_G = -pred_fake.mean()

        optim_G.zero_grad()
        loss_G.backward()
        optim_G.step()

        if epoch % 5 == 0:
            viz.line([[loss_D.item(), loss_G.item()]], [epoch], win='loss', update='append')
            generate_image(D, G, x_r, epoch)
            print(loss_D.item(), loss_G.item())


if __name__ == '__main__':
    main()

这里定义了一个主函数（其实不必叫main，这里不是C/C++）。其中设置随机种子可以大幅缩小随机性，从而降低出现训练不稳定的概率（降低，不是消除，还是会发生的），并且选择了自动梯度下降器Adam来优化目标函数。

在这个嵌套循环中，内层循环是针对判别器训练的，跳出内嵌循环后才执行外层循环内的其余代码，这就体现了前面提到的先训练判别器后训练生成器的思路。注意这里有一个细节，内层循环中其实也有针对生成器的处理x_f = G(z).detach()，detach方法是用于消除其可导性，是要求计算机将其看作一个标量来处理，不对其求梯度，这样就可以避免误训练生成器的问题。另外原作者指出，经常习惯将优化器清零是一种好习惯。

这段代码还有一个技巧——利用梯度下降器求极/最大值。

loss_r = -pred_r.mean()、loss_G = -pred_fake.mean()这两行便体现了这一技巧。

实质上是数学思想的图形变换思想。

六、实现GAN要注意什么？

其实起初在照着原作者所写的写代码，结果一个比较奇怪的问题发生了：

TypeError: can't convert cuda:0 device type tensor to numpy. Use Tensor.cpu() to copy the tensor to host memory first.

分析这个报错信息可知，问题可追溯到generate_image函数这里。根据这一情况可知这样使用cuda是不能继续运行的，按照它的提示，在generate_image函数内将x_r移植到cpu上（上部分是已经完善好的）。

至此程序可以正常运行。

七、“睿智”作者有什么话说？

我已经将这段代码共享了，按自己的理解做了简单的改动，或许有一天我还会继续优化更新。。。。（嗯，我又许下了一个不可能的承诺）

Jupyter Notebook/Lab--->·open in new window

Python--->·open in new window

Generative Adversarial Networks

# 一、什么是GAN？

# 二、GAN能做什么？效果如何？

# 三、GAN的组成是什么？

# 四、GAN的原理是什么？

# 五、GAN如何实现？

# 六、实现GAN要注意什么？

# 七、“睿智”作者有什么话说？