WGAN with Gradient Penalty

Breeze Shane大约 3 分钟

WGAN with Gradient Penalty

结果

WGAN-gp运行效果比上回的WGAN和Original GAN要好多了，不是一点！

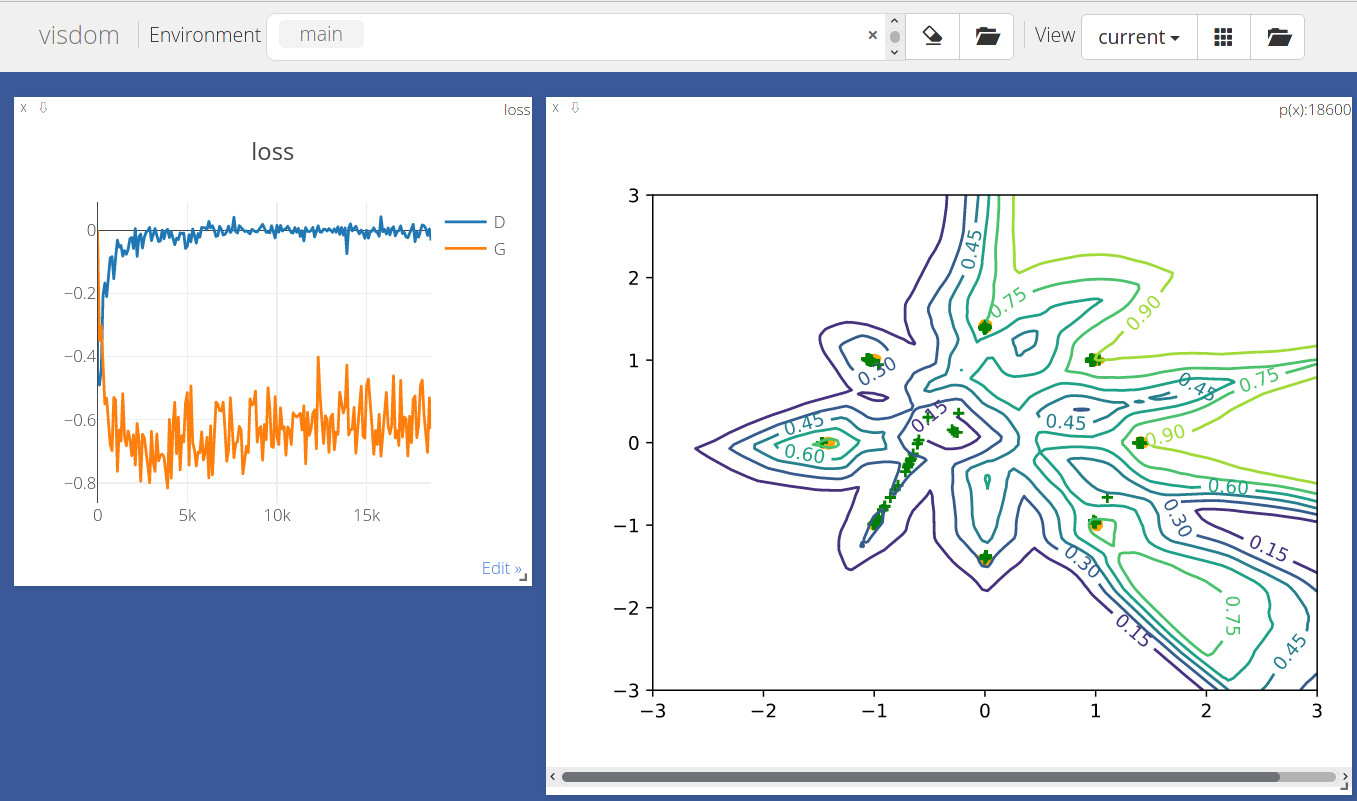
可以看得出来它表现优良，绝大部分点都聚集在各自给定的黄点周围，足见WGAN-GP表现的优异。

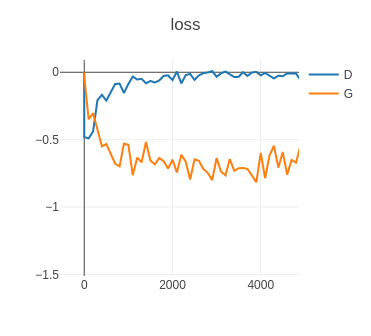
从图像中可以看出来，Loss-D损失函数值不断上升，这说明生成器已经开始成功欺骗了判别器，并且Loss-G损失函数值也在不断下降，说明生成器的仿真度越来越高，生成的数据越来越逼真，也越来越容易欺骗判别器。

上一篇文章比较详细系统地剖析了WGAN，这里就不多做赘述。WGAN以切片形式处理数据时出现了一些问题，比如训练不稳定、准确率不高、梯度爆炸或消失，还有切片参数设置困难等问题。「切片参数设置困难指的是切片上下限难以合适设定，过小则容易将网络转化成二值网络，过大则不起作用。」为了解决这些，有人提出了改良WGAN的一种方法——增加惩罚项。

解决～

为了解决以上的问题，WGAN又有了新的进展，这个新版WGAN不需要权重裁切，采取了加入惩罚项的方式。新版WGAN目标函数定义如下：

W(P_r, P_g)=\max_{D} \{E_{x \sim P_r}[D(x)]-E_{x\sim P_g(x)}[D(x)]-\lambda\int_x\max(0,||\nabla_x D(x)||-1)dx \}

根据 $D(x)$ 的定义显然有 $D(x)\in[0,1]$ 成立，因此对于 $\forall x,\quad||\nabla_x D(x)||\leq1$ 。求积分的形式又可以写成期望的形式，因此该公式又可以写成：

W(P_r, P_g)=\max_{D} \{E_{x \sim P_r}[D(x)]-E_{x\sim P_g(x)}[D(x)]-\lambda E_{x\sim P_{input}(x)}\max(0,||\nabla_x D(x)||-1) \}

其中 $P_{input}(x)$ 是输入数据的分布。

而对于采样的过程，新版WGAN给出的方案是依次从两个分布中各选取一个样本，然后连接两个样本，并在该线段上任意采取一点作为 $P_{input}(x)$ 。正是有 $P_{input}(x)$ 的存在，梯度变化就被约束而平缓变化了。

不过在实现中我们没有直接使用 $\max(0,||\nabla_x D(x)||-1)$ 的形式，因为这个无法直接计算，我们采用的是 $(||\nabla_xD(x)||-1)^2$ 。这意味着我们正要求 $\nabla_xD(x)$ 尽可能接近1，到这里你可能还不明白为什么这样。

首先一定要清晰的是 $D(x)$ 的存在就是为了增大损失函数的值，那么根据上面给的表达式，不难看出，当 $P_r$ 尽可能大，而 $P_g$ 尽可能小的时候损失函数的值必然会尽可能大。这时再回顾 $D(x)$ 的定义，我们会发现这样的变化会导致 $D(x)$ 尽可能接近1。到此为止，我们总算清楚为何要如此做法了。

于是我们最终的损失函数就出炉了：

W(P_r, P_g)=\max_{D} \{E_{x \sim P_r}[D(x)]-E_{x\sim P_g(x)}[D(x)]-\lambda E_{x\sim P_{input}(x)}[(||\nabla_x D(x)||-1)^2] \}

实现！

「注」：以下一切操作均基于Original GAN而修改！

def weights_init(m):
    if isinstance(m, nn.Linear):
        # m.weight.data.normal_(0.0, 0.02)
        nn.init.kaiming_normal_(m.weight)
        m.bias.data.fill_(0)

def gradient_penalty(D, x_r, x_f):
    t = torch.rand(batchsz, 1).cuda()
    t = t.expand_as(x_r)
    mid = t * x_r + (1 - t) * x_f
    mid.requires_grad_()
    
    pred = D(mid)
    grads = autograd.grad(outputs=pred, \
                          inputs=mid, \
                          grad_outputs=torch.ones_like(pred), \
                          create_graph=True, \
                          retain_graph=True, \
                          only_inputs=True)[0]
    
    gp = torch.pow(grads.norm(2, dim=1) - 1, 2).mean()
    
    return gp

定义完这两个函数之后需要在main()中loss_D = loss_r + loss_f改成loss_D = loss_r + loss_f + 0.2 * gp，其中0.2是一种超参数，可以自行调整；并且在这行代码前面加上gp = gradient_penalty(D, x_r, x_f.detach())，并且在定义G、D变量的后面加上G.apply(weights_init和 D.apply(weights_init)这两行代码。

这样我们就完成了WGAN-gp的实现，完整代码请点击这里-->·open in new window

WGAN with Gradient Penalty

# WGAN with Gradient Penalty

# 结果

# 解决～

# 实现！

WGAN with Gradient Penalty

结果

解决～

实现！