本文记录了 LPIPS、SSIM、MAE、MSE、PSNR、NIQE 和 NIMA 共计七个低照度指标,除了介绍相关背景、意义,也会提及算法实现的大致过程。
全称:Learned Perceptual Image Patch Similarity,中文:学习感知图像块相似度,又称感知损失
是用于度量两张图像差别的一种指标,最开始由论文《The Unreasonable Effectiveness of Deep Features as a Perceptual Metric》提出。
LPIPS 值越低,表示两张图像越相似,反之则差异越大。
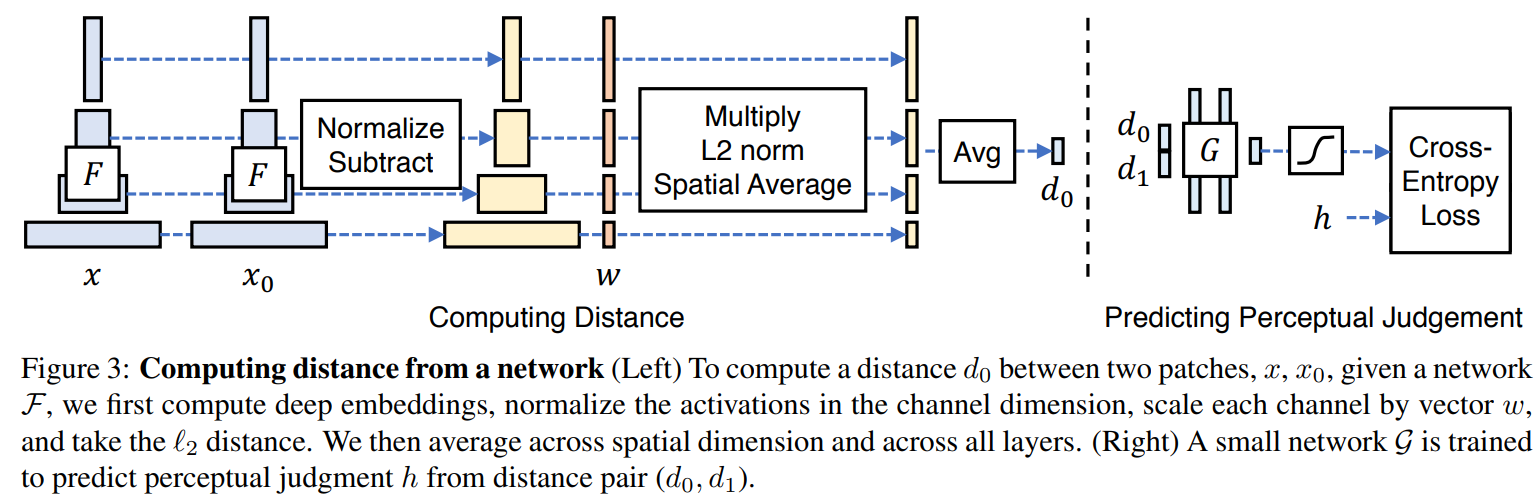
给定 Ground Truth 图像参照块x x x x 0 x_0 x 0
感知相似度度量公式如下:
d ( x , x 0 ) = ∑ l 1 H l W l ∑ h , w ∣ ∣ w l ⊙ ( y ^ h w l − y ^ 0 h w l ) ∣ ∣ 2 2 d(x,x_0)=\sum_l\frac{1}{H_lW_l}\sum_{h,w}||w_l\odot(\hat{y}_{hw}^l-\hat{y}_{0hw}^l)||_2^2 d ( x , x 0 ) = l ∑ H l W l 1 h , w ∑ ∣∣ w l ⊙ ( y ^ h w l − y ^ 0 h w l ) ∣ ∣ 2 2
其中,d d d x 0 x_0 x 0 x x x L L L w l w_l w l L 2 L_2 L 2
网络结构如下:
Network Architecture 基于学习的相似度得分损失函数公式如下:
L ( x , x 0 , x 1 , h ) = − h log G [ d ( x , x 0 ) , d ( x , x 1 ) ] − ( 1 − h ) log { 1 − G [ d ( x , x 0 ) , d ( x , x 1 ) ] } \mathcal{L}(x,x_0,x_1,h)=-h\log\mathcal{G}[d(x,x_0),d(x,x_1)]-(1-h)\log\{1-\mathcal{G}[d(x,x_0),d(x,x_1)]\} L ( x , x 0 , x 1 , h ) = − h log G [ d ( x , x 0 ) , d ( x , x 1 )] − ( 1 − h ) log { 1 − G [ d ( x , x 0 ) , d ( x , x 1 )]}
给定 Ground Truth 图像参照块x x x x 0 x_0 x 0 d 0 d_0 d 0 x x x x 1 x_1 x 1 d 1 d_1 d 1 G \mathcal G G h h h
依照个人理解这里的h h h G [ d ( x , x 0 ) , d ( x , x 1 ) ] \mathcal{G}[d(x,x_0),d(x,x_1)] G [ d ( x , x 0 ) , d ( x , x 1 )] L \mathcal{L} L 信息量存储下来需要多少存储空间 」,由于事件空间只有两种状态,对应的概率为{ p , 1 − p } \{p,1-p\} { p , 1 − p } p ( x ) p(x) p ( x ) p ′ ( x ) p^\prime(x) p ′ ( x ) G [ d ( x , x 0 ) , d ( x , x 1 ) ] \mathcal{G}[d(x,x_0),d(x,x_1)] G [ d ( x , x 0 ) , d ( x , x 1 )] 1 − G [ d ( x , x 0 ) , d ( x , x 1 ) ] 1-\mathcal{G}[d(x,x_0),d(x,x_1)] 1 − G [ d ( x , x 0 ) , d ( x , x 1 )] x 0 , x 1 x_0,x_1 x 0 , x 1
全称:Structural Similarity Index,中文:结构相似性指数
**是一种用于量化两幅图像间的结构相似性的指标。**它仿照了人类视觉系统实现了结构相似性的有关理论,对局部结构变化的感知敏感。SSIM 分别用均值来估计亮度,用方差来估计对比度,用协方差来估计结构相似程度。它的值域是[0,1],而且当SSIM=1时,两张图片完全一致。
给定两张图片 A 和 B ,两者之间的照明度 (luminance)、对比度 (contrast) 和结构 (structure) 分别如下公式所示:
l ( x , y ) = 2 μ x μ y + c 1 μ x 2 + μ y 2 + c 1 c ( x , y ) = 2 σ x σ y + c 2 σ x 2 + σ y 2 + c 2 s ( x , y ) = σ x y + c 3 σ x σ y + c 3 \begin{align} l(x,y)&=\frac{2\mu_x\mu_y+c_1}{\mu_x^2+\mu_y^2+c_1}\\ c(x,y)&=\frac{2\sigma_x\sigma_y+c_2}{\sigma_x^2+\sigma_y^2+c_2}\\ s(x,y)&=\frac{\sigma_{xy}+c_3}{\sigma_x\sigma_y+c_3} \end{align} l ( x , y ) c ( x , y ) s ( x , y ) = μ x 2 + μ y 2 + c 1 2 μ x μ y + c 1 = σ x 2 + σ y 2 + c 2 2 σ x σ y + c 2 = σ x σ y + c 3 σ x y + c 3
一般地,有:
c 3 = c 2 2 c_3= {c_2\over2} c 3 = 2 c 2 μ x \mu_x μ x x x x μ y \mu_y μ y y y y σ x 2 \sigma_x^2 σ x 2 x x x σ y 2 \sigma_y^2 σ y 2 y y y σ x y \sigma_{xy} σ x y x x x y y y c 1 = ( k 1 L ) 2 c_1=(k_1L)^2 c 1 = ( k 1 L ) 2 c 2 = ( k 2 L ) 2 c_2=(k_2L)^2 c 2 = ( k 2 L ) 2 L L L 2 B − 1 2^B-1 2 B − 1 k 1 = 0.01 k_1=0.01 k 1 = 0.01 k 2 = 0.03 k_2=0.03 k 2 = 0.03 而 SSIM 被定义为:
S S I M ( x , y ) = [ l ( x , y ) α ⋅ c ( x , y ) β ⋅ s ( x , y ) γ ] SSIM(x,y)=[l(x,y)^\alpha \cdot c(x,y)^\beta\cdot s(x,y)^\gamma] SS I M ( x , y ) = [ l ( x , y ) α ⋅ c ( x , y ) β ⋅ s ( x , y ) γ ]
令α = β = γ = 1 \alpha=\beta=\gamma=1 α = β = γ = 1
S S I M ( x , y ) = ( 2 μ x μ y + c 1 ) ( 2 σ x y + c 2 ) ( μ x 2 + μ y 2 + c 1 ) ( σ x 2 + σ y 2 + c 2 ) SSIM(x,y)=\frac{(2\mu_x\mu_y+c_1)(2\sigma_{xy}+c_2)}{(\mu_x^2+\mu_y^2+c_1)(\sigma_x^2+\sigma_y^2+c_2)} SS I M ( x , y ) = ( μ x 2 + μ y 2 + c 1 ) ( σ x 2 + σ y 2 + c 2 ) ( 2 μ x μ y + c 1 ) ( 2 σ x y + c 2 )
用于计算平均绝对误差,用来衡量两图片之间的差距,但由于绝对值符号的存在,求得的导数并不平滑,有些点导数不存在,因此不适合作为 Loss,但它能很好地衡量差距。
对于给定的两个图片x x x y y y
M A E ( x , y ) = 1 W × H ∑ i = 0 W − 1 ∑ j = 0 H − 1 ∣ x ( i , j ) − y ( i , j ) ∣ MAE(x,y)={1\over W\times H}\sum_{i=0}^{W-1}\sum_{j=0}^{H-1}|x(i,j)-y(i,j)| M A E ( x , y ) = W × H 1 i = 0 ∑ W − 1 j = 0 ∑ H − 1 ∣ x ( i , j ) − y ( i , j ) ∣
用于计算平均平方误差,用来衡量两图片之间的差距,平方的特性能很好地解决MAE导数不平滑问题,因此它既可以用作 Loss 的指导参考,又可以衡量差距。
对于给定的两个图片x x x y y y
M S E ( x , y ) = 1 W × H ∑ i = 0 W − 1 ∑ j = 0 H − 1 [ x ( i , j ) − y ( i , j ) ] 2 MSE(x,y)={1\over W\times H}\sum_{i=0}^{W-1}\sum_{j=0}^{H-1}[x(i,j)-y(i,j)]^2 MSE ( x , y ) = W × H 1 i = 0 ∑ W − 1 j = 0 ∑ H − 1 [ x ( i , j ) − y ( i , j ) ] 2
全称:Peak Signal to Noise Ratio,中文:峰值信噪比
PSNR 是一种评价图像质量的度量标准,但只是衡量最大值信号和背景噪音之间的图像质量参考值,具有局限性。PSNR的单位为dB,值越大对应图像的失真越少。
提示
一般来说,PSNR 高于40dB说明图像质量几乎与原图一样好;在30-40dB之间通常表示图像质量的失真损失在可接受范围内;在20-30dB之间说明图像质量比较差;PSNR 低于20dB说明图像失真严重。
给定一个大小为W×H的灰度图I I I K K K
P S N R = 10 log 10 ( M A X I 2 M S E ) PSNR = 10\log_{10}(\frac{MAX_I^2}{MSE}) PSNR = 10 log 10 ( MSE M A X I 2 )
其中M A X I MAX_I M A X I M A X I 2 MAX_I^2 M A X I 2 2 B − 1 2^B-1 2 B − 1
有三种方法来计算彩色RGB图像的PSNR:
分别计算 RGB 三个通道的 PSNR,然后取平均值; 计算 RGB 各个通道的均方差的均值,然后统一求 PSNR; 把 RGB 转化为 YCbCr,然后只计算 Y(亮度)分量的 PSNR。 全称:Naturalness Image Quality Evaluator,中文:自然图像质量评估
NIQE是ECCV 2018年PIRM比赛时的评价指标,是一种新的无参考 图像质量指标。其原理与BRUSQUE一致,因为两者皆出自同一人之手。
前面36个特征提取方法几乎一模一样,但 NIQE 在提取图像统计特征时先对图像提取了感兴趣区域,这一点源自于人眼更倾向于以图像中更清晰的部分来判断图像质量。所以作者通过计算图像中不同patch的方差场来判别清晰度,选择大于一定阈值的清晰度为自然图像的patch,而失真图像采用全局计算NSS。
NIQE的建模过程比较复杂,分五大部分:
一、Spatial Domain NSS 提取图像空间域特征
首先将图片进行归一化处理,得到 MSCN 系数:
I ^ ( i , j ) = I ( i , j ) − μ ( i . j ) σ ( i , j ) + 1 \hat{I}(i,j)=\frac{I(i,j)-\mu(i.j)}{\sigma(i,j)+1} I ^ ( i , j ) = σ ( i , j ) + 1 I ( i , j ) − μ ( i . j )
该式表示高斯滤波后求局部均值和局部标准差,其中,
局部均值是对原始图像做高斯模糊处理,具体公式为:
μ ( i . j ) = ∑ k = − K K ∑ l = − L L w k , l I ( i + k , j + l ) \mu(i.j)=\sum_{k=-K}^K\sum_{l=-L}^L{w_{k,l}I(i+k,j+l)} μ ( i . j ) = k = − K ∑ K l = − L ∑ L w k , l I ( i + k , j + l )
局部标准差是对原始图像和局部均值的差的平方做高斯模糊处理,具体公式为:
σ ( i , j ) = ∑ k = − K K ∑ l = − L L w k , l [ I ( i + k , j + l ) − μ ( i , j ) ] 2 \sigma(i,j)=\sqrt{\sum_{k=-K}^K\sum_{l=-L}^L{w_{k,l}[I(i+k,j+l)}-\mu(i,j)]^2 } σ ( i , j ) = k = − K ∑ K l = − L ∑ L w k , l [ I ( i + k , j + l ) − μ ( i , j ) ] 2
二、Patch Selection 筛选图像块
由于人类似乎更重视他们对清晰图像区域的图像质量判断。我们使用一个简单的设备从一组自然补丁中优先选择那些信息最丰富且不太可能受到限制失真的补丁。因此我们的筛选标准是:边缘更锐利的,包含信息内容更丰富的。
在归一化后,筛选前,作者将图像分成大小为P × P P\times P P × P b = 1 , 2 , 3 , . . . , B b = 1,2,3,...,B b = 1 , 2 , 3 , ... , B
δ ( b ) = ∑ ∑ ( i , j ) ∈ p a t h b σ ( i , j ) \delta(b)=\sum\sum_{(i,j)\in pathb}\sigma(i,j) δ ( b ) = ∑ ( i , j ) ∈ p a t hb ∑ σ ( i , j )
这里的δ \delta δ
在做筛选的时候,作者将所有的图像块的最大锐利程度的p倍设置为阈值,其中p ∈ [ 0.6 , 0.9 ] p\in [0.6, 0.9] p ∈ [ 0.6 , 0.9 ]
三、Characterizing Image Patches 求图像块特征
该部分用到 GGD (广义高斯分布) 和 AGGD (非对称广义高斯分布) 求图像块特征,首先利用 GGD 求取图像的两个特征:
f ( x , α , β ) = α 2 β Γ ( 1 α ) e x p [ − ( ∣ x ∣ β ) α ] Γ ( a ) = ∫ 0 ∞ t a − 1 e − t d t a > 0 \begin{align*} f(x,\alpha,\beta)&=\frac{\alpha}{2\beta\,\Gamma({1\over\alpha})}\, exp[-(\frac{|x|}{\beta})^\alpha] \\ \Gamma(a)&=\int_0^\infty t^{a-1}e^{-t}\, dt\qquad a>0 \end{align*} f ( x , α , β ) Γ ( a ) = 2 β Γ ( α 1 ) α e x p [ − ( β ∣ x ∣ ) α ] = ∫ 0 ∞ t a − 1 e − t d t a > 0
并且使用了快速匹配算法得到了参数α \alpha α β \beta β
四、Multivariate Gaussian Model 多元高斯模型
已知有拟合高斯模型(MVG):
f X ( x 1 , … , x k ) = 1 ( 2 π ) k 2 ∣ ∑ ∣ 1 2 × e x p [ − 1 2 ( x − ν ) T Σ − 1 ( x − ν ) ] f_X(x_1,\,\dots\,,x_k)=\frac{1}{(2\pi)^{k\over2}|\sum|^{1\over2}}\times exp\big[ -{1\over2}(x-\nu)^T\Sigma^{-1}(x-\nu) \big] f X ( x 1 , … , x k ) = ( 2 π ) 2 k ∣ ∑ ∣ 2 1 1 × e x p [ − 2 1 ( x − ν ) T Σ − 1 ( x − ν ) ]
输入每张清晰图像的特征参数后得到上式,对其做最大似然估计后将得到该模型的均值向量ν \nu ν Σ \Sigma Σ
五、NIQE Index 最终得分
D ( ν 1 , ν 2 , Σ 1 , Σ 2 ) = ( ν 1 − ν 2 ) T ( Σ 1 + Σ 2 2 ) − 1 ( ν 1 − ν 2 ) D(\nu_1,\nu_2,\Sigma_1,\Sigma_2)=\sqrt{ (\nu_1-\nu_2)^T\,\big(\frac{\Sigma_1+\Sigma_2}{2}\big)^{-1}(\nu_1-\nu_2) } D ( ν 1 , ν 2 , Σ 1 , Σ 2 ) = ( ν 1 − ν 2 ) T ( 2 Σ 1 + Σ 2 ) − 1 ( ν 1 − ν 2 )
由上式即可得出最终得分,ν 1 \nu_1 ν 1 Σ 1 \Sigma_1 Σ 1 ν 2 \nu_2 ν 2 Σ 2 \Sigma_2 Σ 2